1.0 Stabilitet og belastning i stille vann

Fig. 1.01 Det Singaporeregistrerte skipet Cougar Ace hadde 4.813 biler om bord, og skulle til Canada. Cougar Ace eies av et japansk selskap, og er 654 fot (200 meter) langt. Om kvelden 23.07.06 fikk skipet stadig større slagside nær øygruppen Aleutene, og mannskapet på 23 måtte evakueres i tung sjø. (Mannskapet kunne ikke si noe om årsaken til krengningen skyldtes innsig/lekkasje av sjøvann, eller overløpsvann fra ballasttankene.) Fartøyet ble reddet på mirakuløst vis, og buksert inn til Portland. (Foto: U.S. Coast Guard/AP – The Cargo Letter 2006)
1.1 Mål for stabilitet i stille vann, et tilbakeblikk
Når et skip krenger over som følge av en ytre belastning (eller usymmetrisk vektfordeling om bord), blir oppdriftssenteret B flyttet tverrskips, inntil det oppstår likevekt mellom de krengende og de rettende momentene, som vist på figur 1.02:
∆·GZ=P·a (1.01)
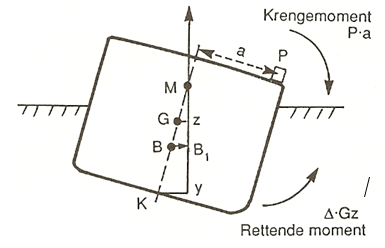
Fig. 1.02 Likevekt mellom de krengende og rettende momenter. (Wilhelmsen 1996)
Det rettende momentet uttrykker skipets evne til å motstå krengning, og fordi oppdriften Δ endrer seg med skipsstørrelsen, gir den rettende armen GZ et mål for skipets stabilitet.
Oppdriftssenterets plassering m.h.t. det krengende skipet, blir bare bestemt av geometrien i den delen av skroget som er neddykket. Det vil si at B flytter seg mot lav side og øker GZ så lenge det effektive oppdriftsvolum blir trykket ned i vannet på lav side.
GZ-armen omfatter stabilitetsegenskaper som er knyttet både til skipets form og vektplassering. Den er derfor et godt mål for skipets evne til å motstå krengemoment. GZ beregnes fra skipets KY-kurver (cross curves):
(1.02)
1.11 Initialstabilitet (eller begynnelsesstabilitet).
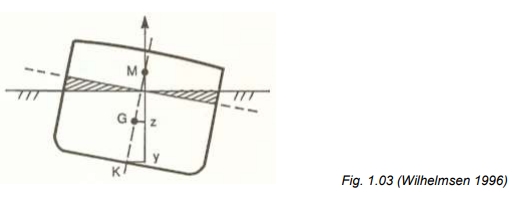
Ved små krengevinkler er den delen av skroget som blir trykket ned i vann tilnærmet lik den delen som kommer ut av vannet ved en gitt krengning. Dette forutsetter rette, vertikale skipssider (wall-sided) og en jevn linjeføring mot endene av skipet på den aktuelle vannlinjen. Av fig. 1.03 fremgår det da at:
(1.03)
– initialmetasenterhøyden – kan nyttes som et mål for stabilitet ved små krengninger, opp til ca. 7° (under forutsetning av rette, vertikale skipssider), og gir et uttrykk for skipets «stivhet», dvs. motstand mot krengning på rett kjøl.
Meta betyr mellom på gresk og angir her forflytning, dvs. at senteret ikke ligger fast. Z = zero (null). Z er nullpunktet for normalen fra G.
(1.04)
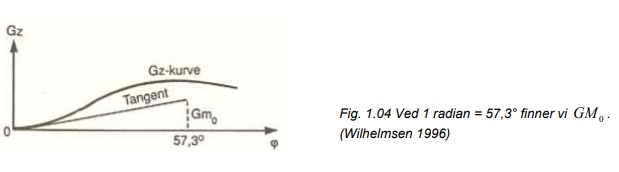
Vi finner tilnærmet størrelsen på av GZ-kurven ved å trekke tangenten til kurven gjennom origo (stigningskoeffisienten).
Ved 1 radian = 57,3° finner vi (fig. 1.04). Metoden kan være upålitelig da den er basert på rette skipssider.
Vinkelen angis i grader på diagrammene, men inngår alltid i beregningene i radianer. Vi har stabilt skip når skipet ligger i stabil likevekt i rett stilling. Betingelsen for dette er at GM er positiv, dvs. at metasenteret M ligger over G. Metasenteret er funnet fra følgende formel:
KM = KB + BM (1.05)
hvor metasenterets høyde over oppdriftssenteret: , og hvor I er treghetsmomentet til vannlinjeplanet (tverrskips). Det er vanlig å angi I som:
hvor
er en faktor som avhenger av vannlinjeplanets form, L er skipets lengde mellom perpendikulærene (Lpp), og B er bredden i vannlinjen. For et rektangulært vannlinjeplan er
og vi kan angi I som:
. For store tankskip i lastet tilstand vil treghetskoeffisienten for vannlinjeplanet ligge nær 1/12. (Tellnes 2001)
1.12 Krav til stabilitet i stille vann.
Disse krav gjelder for skip med L < 100 m. For skip med L > 100 m vurderer Sjøfartsdirektoratet stabiliteten i hvert enkelt tilfelle. Kravene følger stort
sett de samme reglene som for skip med L < 100 m:
- Arealet under GZ-kurven som angir den rettende arm, skaI ikke være mindre enn 0,055 meter-radianer regnet opp til en krengningsvinkel på 30° og ikke mindre enn 0,09 meter-radianer regnet opp til en krengningsvinkel på 40°, eller til fyllingsvinkelen (til dit hvor vann kan trenge inn) dersom denne er mindre enn 40°. Dessuten skal arealet under stabilitetskurven (GZ-kurven) mellom 30° og 40°, eller mellom 30° og fyllingsvinkelen dersom denne er mindre enn 40°, ikke være mindre enn 0,03 meter-radianer.
- GZ-armen skal minst være 0,20 meter ved en krengningsvinkel lik eller større enn 30°.
- Den krengningsvinkel hvor den rettende arm (GZ) har størst verdi, bør være større enn 30° og skal aldri være mindre enn 25°.
- Metasenterhøyden (GM) skal minst være 0,15 meter.
Alle disse stabilitetskrav skal basere seg på den mest ugunstige situasjon angående fulle eller tomme tanker osv. ombord på reisen.
1.13 Tverrskipsstabilitet ved større krengninger.
sier ikke noe om skipets stabilitetsforhold ved større krengninger. Vi vet at for fartøyer som blir utsatt for større krengninger, vil oppdriftssenteret flytte seg så langt ut at oppdriftslinjen ikke lenger går gjennom initialmetasenteret M, og vi må operere med
= det falske metasenteret, se fig. 1.05.
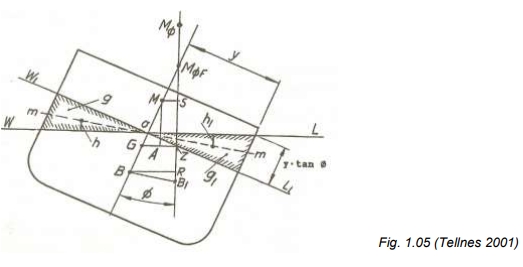
Ut fra den nye vannlinjen vil metasenteret ligge i .
Skjæringspunktet med senterlinjen blir (det falske metasenteret).
Vi ser at:
(1.06)
Størrelsen MS kalles reststabiliteten.
Fig. 1.04 viser at tangenten til GZ i origo angir GM ved ø = 57,3°. Av (1.06) får vi, når ø0:
 (1.07)
(1.07)
Den deriverte av GZ med hensyn på ø gir vinkelkoeffisienten i origo, dvs. tangenten til kurven i origo:
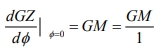
Ved å trekke tangenten til kurven i origo og sette ø =1 radian = 57,3° finner vi GM (fig. 1.04). (Altså; den deriverte av GZ for ø = 0 er GM, hvilket gir at vinkelkoeffisienten til GZ-kurven er GM)
1.14 Reststabiliteten MS
Av fig 1.06 fremkommer uttrykket (Tellnes 2001), som betyr at avstanden
= det falske metasenteret:
(1.08)
og reststabiliteten:
(1.09)
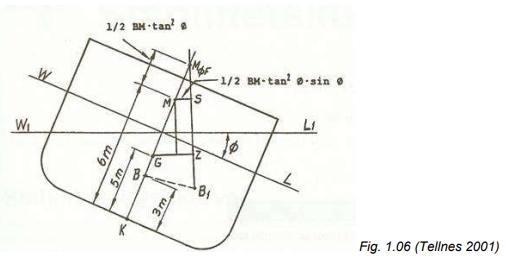
hvor kommer som et tillegg i GZ-armen,
, hvor metasenterhøyden GM er et mål for initialstabiliteten, og MS for reststabiliteten. For krengevinkler < 10-12° settes dette leddet = 0. Formelen brukes til å beregne GZ til at krengevinkelen blir så stor at dekket kommer i vannflaten. For krengevinkler større enn dette brukes andre metoder.
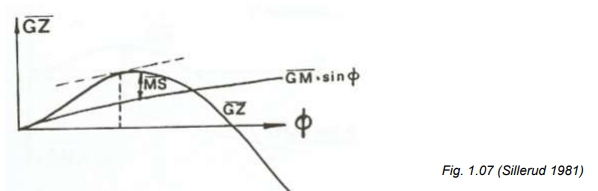
Når dekkshjørnet kommer i vannflaten, vil MS-kurven normalt være i nærheten av sin maksimalverdi. På fig. 1.07 er vist hvorledes denne vinkelen finnes ved å trekke en tangent til GZ-kurven parallell med kurven . (Sillerud 1981)
1.15 Dynamisk stabilitet
Arealet under GZ-kurven ved en gitt krengning gir et uttrykk for det arbeidet som må utføres for å krenge skipet.
Dynamisk stabilitet defineres som den energien som skal til for å krenge et skip fra 0° til vinkelen ø.
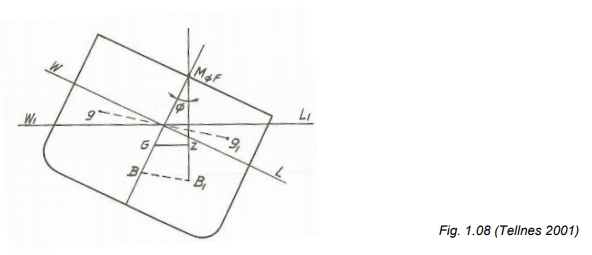
Av fig. 1.08 ser en at når skipet ligger på rett kjøl, virker tyngden av skipet nedover i G og oppdriften oppover i B. Når skipet krenger, blir G løftet i forhold til B. Skipet har blitt løftet en vertikal avstand lik. Det arbeid som kreves for å utføre dette, er:
(1.10)
hvor enheten er Nm . For å utføre dette arbeidet må skipet tilføres en energi som er like stor. Denne energien lagres i skipet, og er et mål for det samlede arbeid skipet yter mot krengningen. Pr. definisjon er dynamisk stabilitet lik denne energien. Arealet finner vi ved å integrere GZ-kurven. Dynamisk stabilitet kan da skrives som (Tellnes 2001):
(1.11)
hvor enheten er Nm . Vinkelen er gitt i radianer, og i praksis benyttes tonnmeter. Formelen kan skrives som:
 (1.12)
(1.12)
hvor er arealet under GZ-kurven i meterradianer.
Dynamisk stabilitet ved en gitt krengevinkel er proporsjonal med arealet under GZ-kurven (og skipets størrelse gitt ved ) opp til denne krengevinkelen. Siden de krengende momenter skipet blir utsatt for også vil øke med størrelsen av vind- og sjøgangskrefter, er det i stedet vanlig å angi den dynamiske stabilitetsarmen e, som gir et mål for arealet under GZ-kurven til gitt krengning uttrykt i meterradianer eller metergrader:
(1.13)
Den dynamiske stabilitetsarmen = arealet under GZ-kurven, se fig. 1.09 (Tellnes 2001)
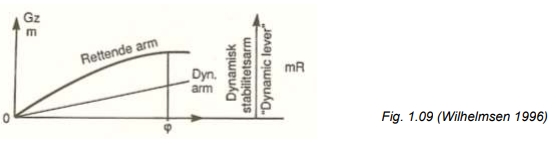
Arealet under GZ-kurven er et mål på skipets motstand mot krengning, og det er selvsagt viktig at denne er stor nok til å sikre at skipet ikke kantrer.

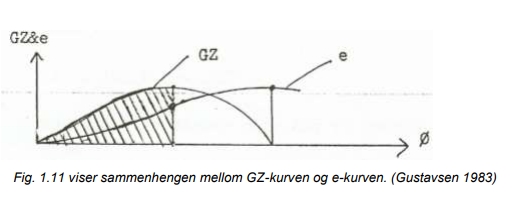
Når vi betrakter fig. 1.10 ser vi at ved:
A < B har vi et stabilt skip
A = B har vi et indifferent skip
A > B har vi et ustabilt skip
1.16 Formstabilitet
Sentrale faktorer for et skips stabilitetsegenskaper er som nevnt
formen på den neddykkede delen av skroget og vektfordelingen om bord. Som nevnt er det bare formen på den delen av skroget som er under vann, som bestemmer plasseringen av oppdriftssenteret. Under krengning vil derfor volumer som bringer B langt utover mot lav side, gi god stabilitet, derav navnet formstabilitet.
Fig. 1.12 a) og b) (Wilhelmsen 1996)
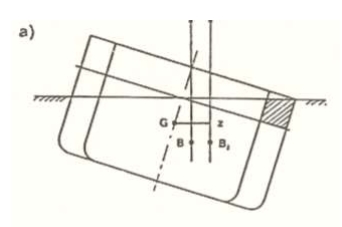
a) Fig. 1.12 a viser to skip med forskjellig bredde. En ser lett at stor bredde gir stort tilskudd til det rettende momentet, derfor kan vi fastslå at stor bredde gir godformstabilitet.
Den heltrukne linjen på fig. 1.12 b viser dekket på et skip med lite fribord,
dekkshjørnet er under vann, og oppdriftssenteret ligger i B.
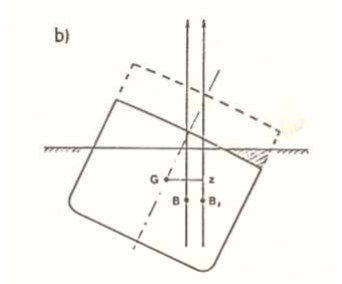
b) Øker vi fribordet som vist med stiplet linje, får vi ekstra oppdrift, og oppdriftssenteret går mot lav side til B1. Stort fribord gir god formstabilitet.
Den stiplede linjen kunne godt vært et lukket overbygg, men oppdriftstilskuddet ville da bare gå over overbyggets lengde. På samme måten virker utpreget spring.
Lukket overbygg gir god formstabilitet.
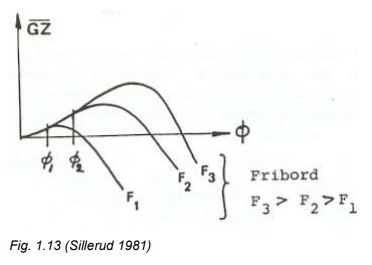
Dersom et skip har stort fribord, vil selvfølgelig MS ha sin maksimale verdi ved en stor krengevinkel. Stort fribord vil derfor bedre MS– og GZ-kurvens utstrekning og høyde.
På fig. 1.13 er skissert GZ-kurver for tre skip som er identiske bortsett fra fribordet (de har samme undervannsskrog, vekttyngdepunkt etc.). GZ-kurvene for skip 1 og 2 skiller lag ved vinkelen ø1, hvor dekkshjørnet til skip 1 kommer i vannflaten. (Sillerud 1981)
1.17 Formstabilitet for 100 år siden.

Fig. 1.14 Denne illustrasjonen fra 1907 er hentet fra et kapittel om stabilitetskurver i Lærebok i sjømandskap, maskinlære med videre, av kommandørkaptein Niels Nickelsen, Horten og sjømandsskolebestyrer O.S. Giertsen, Bergen. (Nickelsen og Giertsen 1907)
1.18 Vektstabilitet.
Som kjent er stabiliteten uttrykt ved GZ-kurven, avhengig av hvor det felles tyngdepunktet G ligger. Lav G gir god vektstabilitet.
1.19 Rulleperiode og stabilitet
Fartøyets naturlige rulleperiode (Egen-svingeperiode = egen-rulleperiode) T varierer med lastkondisjonen, dvs. fartøyets mengde og fordeling av last. Rulleperioden er den tiden fartøyet bruker på å fullføre en fullstendig svingning, fra en ytterstilling til den andre ytterstillingen og tilbake til den opprinnelige. Et fartøy som ruller, kan tilnærmet sammenlignes med en fysisk pendel som er opphengt i fartøyets metasenter. (Wilhelmsen 1996). Svingetiden for en fysisk pendel er:

hvor rulleperioden er bestemt av fartøyets treghetsmoment om diametralplanet, og dreiemomentet som retter fartøyet opp, dvs. fartøyets stabilitetsmoment. Flere formler er utledet av (1.14). Mye brukt er Weiss’ formel:
(1.15)
hvor koeffisienten f kan bestemmes etter krengnings- eller rulleforsøk. For større fartøy ligger f mellom 0,7 og 0,8. B er fartøyets bredde i vannlinjen.
Denne formelen forteller oss at det er en sammenheng mellom et fartøys stabilitet og oppførsel i sjøen.
Er GM-verdien for stor vil fartøyet være for stivt, og vil kunne få hurtige og dermed ubehagelige og farlige rullebevegelser i sjøen. Er GM-verdien for liten vil fartøyet få langsomme og behagelige rullebevegelser i sjøen. Meget langsom oppretting etter krengning tyder på (for) liten GM-verdi.
1.2 Belastning i stille vann
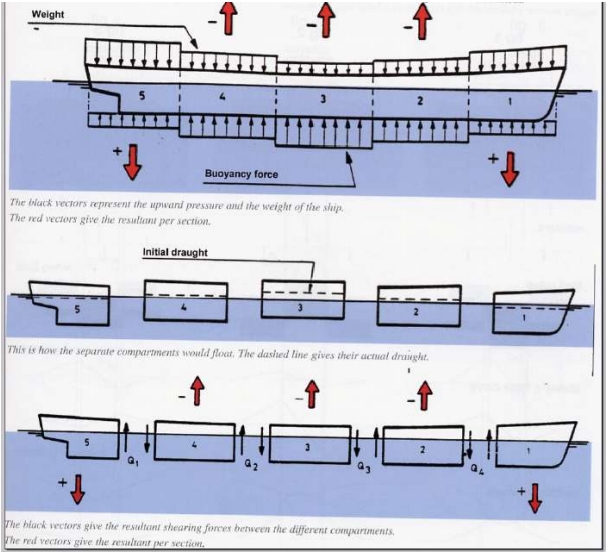
Fig. 1.15 De sorte vektorene viser oppdriftskraften og tyngden på de ulike seksjonene i lett skip. De røde vektorene viser resultantkraften pr. seksjon. I midten ser vi hvorledes seksjonene vil flyte i vannet hver for seg. (Dokkum 2006)
Fig. 1.15 viser horisontale skjærekrefter som virker på lett skip i stille vann som følge av seksjonenes forskjellige oppdriftskraft og tyngde. Resultantkraften pr. seksjon kan mangedobles ved feil lasting og/eller feil ballastering. Dette kan gi uakseptable stabilitets- og trim-kondisjoner, og i verste fall ødelegge skroget.

Fig. 1.16 Undervannsskroget til dette fartøyet viser klart forskjellen i volum mellom midtskipsseksjonen og for- og akterskipet. Dette forklarer tydelig forskjellen i oppdriften på de forskjellige skrogdelene. (Dokkum 2006)