REFERANSESYSTEMET
Her skal vi bli litt bedre kjent med
• jorda og koordinatene
• kvadrantkurser
• fartøyets meridian som peilereferanse
• forandret bredde og lengde, middelbredde og avvikning
• fart, tid og distanse
Øystein Johnsen
Jorda og koordinatene
Kule, geoide eller ellipsoide?
Jorda er tilnærmet formet som en kule, men er flattrykt ved polene. Et legeme som har jordas form kaller vi en ellipsoide. I tradisjonell navigasjon betrakter vi jorda som en kule, noe som likevel gir oss tilstrekkelig nøyaktighet i beregningene våre. Nøyaktigheten vi arbeider innenfor er i størrelsesorden 100 meter eller mer. Begrepet posisjonering benyttes når kravet til nøyaktighet er større, fra noen cm til noen få meter. Jorda roterer om en diameter som vi kaller jordaksen. Der hvor aksen skjærer jordoverflaten, ligger de geografiske polene, Nordpolen og Sydpolen. Jorda roterer fra vest mot øst, og den tiden jorda bruker på en omdreining kaller vi et døgn.
Storsirkler og småsirkler, meridianer og ekvator
En storsirkel er en sirkel på jordkuleoverflaten hvor sirkelens sentrum ligger i kulas sentrum. Den korteste veien mellom to punkter på en kuleoverflate er alltid en del av en storsirkel. En småsirkel er en sirkel hvor sentrum ikke ligger i kulas sentrum.
En meridian er en storsirkel som går gjennom jordas poler. Hvert sted på jorda har sin meridian, stedets meridian, og alle meridianer står vinkelrett på ekvator. Jordas ekvator er en storsirkel som overalt ligger like langt fra Nordpolen som fra Sydpolen. Ekvator deler jorda i den nordlige og den sørlige halvkule.
Meridianen er en storsirkel. En storsirkel har sentrum i kulas sentrum. Meridianene møtes i polene. Lengden regnes i grader fra nullmeridianen 0° til datolinjen 180°.
Parallellsirkler er småsirkler som er parallelle med ekvator. Hvert sted på jorda har sin parallellsirkel, stedets parallellsirkel, og sentrum for alle parallellsirkler ligger i jordaksen. Parallellsirklenes omkrets blir mindre jo lenger vekk fra ekvator de ligger. Vendesirklene er de to parallellsirklene som ligger 23° 26’ på hver side av ekvator. Dette tilsvarer solas størstenord- og sørdeklinasjon (dec). Deklinasjonen har betydning når vi senere skal foreta beregninger i astronomisk navigasjon.
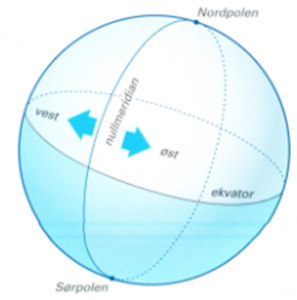
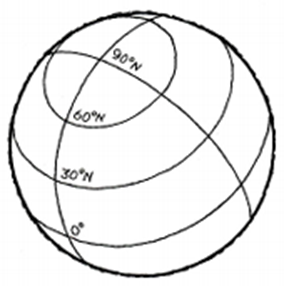
Ekvator er en storsirkel, parallellsirklene til ekvator er småsirkler. Ekvator deler Jorda i den nordlige og sørlige halvkule. Nullmeridianen deler Jorda i den vestlige og østlige halvkule.
Alle meridianer er delt i 90 breddegrader fra ekvator til polene.
Polarsirklene er de to parallellsirklene som ligger 23° 26’ fra polene, 66° 34’ fra ekvator. Alle meridianer er delt i 90 breddegrader (90°) fra ekvator til polene. Hver breddegrad er delt i bueminutter (60’) og hvert bueminutt i sekunder (60’’). Et steds bredde på jorda er stykket av en meridian som går gjennom stedet fra ekvator og til stedets parallellsirkel. Den meridianen som går fra Nordpolen til Sydpolen gjennom Greenwich observatorium utenfor London, kalles nullmeridianen, førstemeridianen eller Greenwich-meridianen. Den danner utgangspunktet for måling av lengde og er også utgangspunktet for tidsmålingen på jorda. Et steds lengde er posisjonen øst (east) eller vest (west) for nullmeridianen. Alle steder som ligger på samme meridian har samme lengde. Lengden regnes i grader fra 0° til 180°, east (E) eller west (W). Vi benytter vanligvis engelske prefikser E og W for å definere øst og vest.
Jordas koordinatsystem
I jordas koordinatsystem er x-aksen ekvator (lgd) og y-aksen nullmeridianen gjennom Greenwich (br). Posisjonen blir gitt som et vinkelmål i forhold til jordas sentrum, og koordinatene beskrives som bredde (br) og lengde (lgd). Står det W030° ved en meridian, betyr det at den er tredve lengdegrader vest for nullmeridianen.
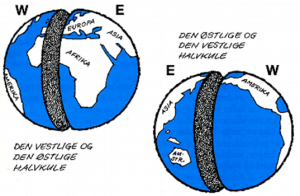
T.v. Sett med våre øyne ligger den vestlige halvkule i vest og den østlige i øst. Når vi ser det fra den andre siden av kloden blir det omvendt. (Ill.: S. Aarset 1997)
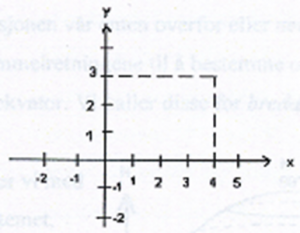
T.h. I jordas kartesiske koordinatsystem (rektangulært koordinatsystem hvor koordinataksene er vinkelrett på hverandre) er x-aksen ekvator (lgd) og y-aksen nullmeridianen gjennom Greenwich (br). (Ill.: S. Løken 2008)
Står det N40° ved en parallellsirkel (gjerne kalt breddesirkel), betyr det at den er førti breddegrader nord for ekvator. Koordinatene der disse to sirklene krysser hverandre angir vi som N40° W030°. Vi bruker alltid to sifre for å angi breddegrad, og tre sifre for å angi lengdegrad. Vi må benytte N, S, E eller W for å gjøre koordinatangivelsen entydig. I stedet for bokstaver vil kalkulatorer og dataprogram normalt bruke minus (-) for S og W.
Lengdemål, retninger og peilinger
En posisjon kan skrives slik: N 62° 25′ 30″ (nord bredde, 62 grader, tjuefem minutter, 30 sekunder) E 005° 40′ 12″ (øst lengde, fem grader, førti minutter, tolv sekunder). Det vanligste er å oppgi minuttene med desimaltall: N 62o 25,5′ E 005° 40,2′. Her blir 25′ 30″ = 25,5′ fordi 30″ : 60″ = 0,5′. Og 40′ 12″ = 40,2′ fordi 12″ : 60″ = 0,2′. Av og til kan vi oppleve at posisjonen blir skrevet i desimalgrader: N 62,425° E 005,67°.
Gradnettet – når vi oppgir koordinatene til et sted, forteller vi hvor langt vi er fra ekvator og nullmeridianen. Koordinatene angis alltid med to sifre i breddeposisjonen og tre sifre i lengdeposisjonen, N40°00’ W030°00’ og S40°00’ E020°00’. Plasseringen av N/S og W/E er valgfri, foran (som vist her), eller bak koordinat-verdien, som f.eks. 40°00’N 030°00’W.
Lengdemål til sjøs
Den internasjonale enheten for lengdemål til sjøs er en nautisk mil (n.mil eller nm). I Norge ble lengden på en nautisk mil fastsatt til eksakt 1852 m ved lov av 29. juni 1923 nr. 3, og Den første internasjonale hydrografiske konferanse i 1929 vedtok bruken av nautisk mil under navnet internasjonal nautisk mil.
Men, hvor lang er egentlig én meter?
Måleenheten meter ble lansert i Frankrike for over to hundre år siden. Den gangen ble en meter definert som en ti-milliondel av avstanden fra Nordpolen til ekvator, i rett linje gjennom Paris. Den første internasjonale prototypen på en meter ble laget i 1889 i en legering av platina og iridium. I dag er én meter definert som avstanden lyset beveger seg i vakuum i løpet av 1/299 792 458 sekund.
Og, hvor langt er egentlig et meridianminutt?
På grunn av at jorda er flattrykt ved polene, blir lengden av et meridianminutt ved ekvator 1842.9 m (WGS 84), ved polene 1861,6 m (WGS 84) og ved 45° bredde 1852,2 m (WGS 84). Avstanden fra en pol til ekvator ble i sin tid definert til l0 000 000 m. Det er 90° fra en pol til ekvator. Hver grad består av 60′, 90° x 60’ = 5400′. Gjennomsnittslengden av et meridianminutt utfra definisjonen av en meter, blir da: 10 000 000 m / 5400′ = 1851,852 m ≈ 1852 m.
Et bueminutt (eng. minute of arc)
Et bueminutt er lik 1/60 av en grad. Ettersom én grad er definert som 1/360 av en full sirkel, er ett bueminutt lik 1/21600 av en full sirkel, som igjen er lik π/10800 radianer.
En radian
En radian er definert som buelengde delt på radius. Radianer er en ubenevnt størrelse, men ofte brukes symbolet rad. 2π • rad = 360°. 1 rad = 180º/π = 57.295779513º. Ved regning med radianer er det vanlig praksis å regne med eksakte tall dersom det er mulig.
En vinkel på 1 radian tilsvarer en vinkel der buelengden er lik radien i en sirkel.
Omregning grader og radianer:
| Grader | 0° | 30° | 45° | 57,2958…° | 60° | 90° | 180° | 270° | 360° |
| Radianer | 0 | π/6 | π/4 | 1 | π/3 | π/2 | π | 3π/2 | 2π |
Sjømil og kvartmil
Før vi begynte med nautiske mil som lengdemål, ble begrepet sjømil brukt. Da metersystemet ble innført i 1875, ble én sjømil definert som lengden av 1⁄15 lengdegrad ved ekvator, som etter den tids beregning ble fastsatt til 7 421,43 m. Begrepet kvartmil, som svarer til ett ekvatorminutt (lengdeminutt langs ekvator), blir da 1855,36 meter. I 1929 ble begrepet nautisk mil innført, og benevnelsene sjømil og kvartmil gikk ut av bruk.
En kabellengde
En kabellengde er en lengdeenhet som har vært brukt til sjøs helt siden 1500-tallet. Opprinnelig målte den 120 favner eller 225,9 meter, senere ble en kabel omdefinert til 1/10 nautisk mil, eller 185,2 m. Engelskmennene derimot, definerer en kabel som 1/10 Sea Mile. Én engelsk Sea Mile er lik ett meridianminutt, én kabel ved ekvator er dermed 184,3 m, ved polene 186,2 m og ved 45° bredde 185,2 m (alle WGS 84).
I tradisjonell navigasjon
I tradisjonell navigasjon betrakter vi jorda som en kule, og vi anser et meridianminutt, eller bueminutt, som likeverdig med:
1. en nautisk mil
2. et ekvatorminutt (et lengdeminutt langs ekvator)
3. et storsirkelminutt
Kvadrantkurser
Kurser, himmelretninger og peilinger
Når vi snakker om retninger til sjøs, tar vi utgangspunkt i sirkelen. Tenk deg at du befinner deg i sentrum av en kompassrose, slik at du har hele horisonten rundt deg. Dette kaller vi den naturlige horisont eller kimmingen. Synsranden blir da delt inn i 360°. Kurslinjen er vinkelen mellom båtens kjøl og stedets meridian. Styrer du langs meridianen – det vil si rett mot nord eller sør – blir det ingen vinkel. Styrer du østover eller vestover, blir vinkelen 90°. På kompassrosen starter vi i nord og beveger oss rundt horisonten med urviseren. Nord er dermed 000° (eller 360°), øst 090°, sør 180° og vest 270°. Mellom de fire hovedretningene har vi nordøst (045°), sørøst (135°), sørvest (225°) og nordvest (315°). Sannsynligvis har du også hørt uttrykkene nord-nordøst (NNE), øst-nordøst (ENE) osv. De stammer fra den gang kompasset ble inndelt i 32 streker som hver var på 11,25°. Nord-nordøst tilsvarte to streker, nordøst fire, øst-nordøst seks og øst åtte. Figuren under viser en kompassrose med inndeling både i grader og streker. Hver strek er igjen delt i kvartstreker. Navnene et påført for hver strek, og vi ser at en strek tilsvarer 11,25°. En annen måte å angi retning på er å telle antall grader fra nord eller sør og korteste veien øst- eller vestover. Vi setter da en bokstav foran og en bak gradtallet for å vise hvor vi teller fra, N eller S, og hvor vi går, W eller E. S 30° W er f.eks. det samme som 210°, og S 30° E er det samme som 150°. N 30° W er lik 330°.
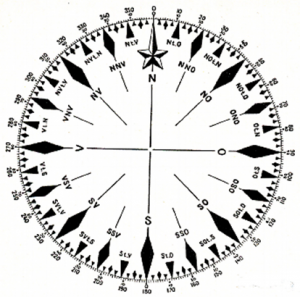Kompassrosen er et forminsket bilde av kimmingen (den naturlige horisonten).
Tre regler for bruk av navigasjonsformler på kalkulator
Når vi entrer navigasjonsformlene på kalkulator må vi holde orden på fortegnsreglene.
- Kurser entres med verdier fra 000° til 360°
- Dersom fortegnet (+) fremkommer i svaret eller entres i formlene, betyr det nord bredde
nord forandret bredde
nord deklinasjon (brukes i astronomisk navigasjon)
øst lengde
øst forandret lengde - Dersom fortegnet (-) fremkommer i svaret eller entres i formlene, betyr det sør bredde
sør forandret bredde
sør deklinasjon (brukes i astronomisk navigasjon)
vest lengde
vest forandret lengde
Kvadrantkurser
Når vi bruker navigasjonsformlene på kalkulator og får positivt eller negativt fortegn foran en kvadrantkurs, er det fornuftig å tegne figurer og orientere disse riktig. Kursvinklene tar utgangspunkt i nord (N) eller syd (S).
Fortegnet forteller oss i hvilke to kvadranter (kv.) vi må vurdere hvor kvadrantkursen ligger. 1. og 4. kv. gir oss en nordlig kurs, mellom 000° – 090° i 1. kv., og mellom 270° – 360° i 4. kv., mens 2. og 3. kv. gir sørlig kurs. 1. og 2. kv. gir oss samtidig østlig kurs, mens 3. og 4. kv. gir oss vestlig kurs.
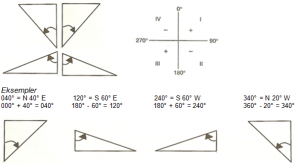
Eller sagt på en annen måte:
N 40° E. Vi tar utgangspunkt i N = 000° og går 40° mot E. Det gir 000° + 40° = 040°.
S 60° E. Vi tar utgangspunkt i S = 180° og går 60° mot E. Det gir 180° – 60° = 120°.
S 60° W. Vi tar utgangspunkt i S = 180° og går 60° mot W. Det gir 180° + 60° = 240°.
N 20° W. Vi tar utgangspunkt i N = 360° og går 20° mot W. Det gir 360° – 20° = 340°.
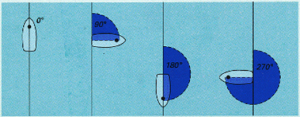Nord er 000° (eller 360°), øst 090°, sør 180° og vest 270°. (Ill.: S. Løken 2008)
Polarkoordinatsystemet
For å kunne styre et fartøy mot et gitt punkt, og samtidig kunne angi en kurs og en avstand til punktet i forhold til fartøyet, eller i forhold til et annet punkt, behøves en annen type koordinatsystem enn det kartesiske. Vi trenger et polarkoordinatsystem der de to koordinatene er en vinkel B regnet fra en viss 0-linje (y-aksen), og en avstand A målt fra origo.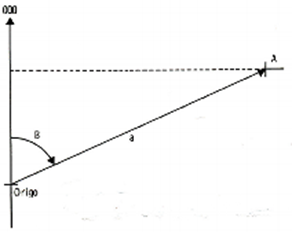
Prinsippet for et polarkoordinatsystem (hvor hvert punkt i et plan er bestemt ut i fra et gitt punkt, vanligvis origo, og vinkel i forhold til y-aksen). De to koordinatene er en vinkel B regnet fra en viss 0-linje (y-aksen), og en avstand A målt fra origo.
Fartøyets meridian som peilereferanse
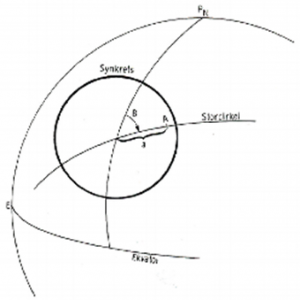Her er vi plassert i en båt i skjæringspunktet mellom storsirkelen og meridianen.
Vinkelen B, vinkelen mellom meridianen gjennom fartøyet og «vår» storsirkel, kalles fartøyets rettvisende kurs og betegnes Rv k, eller RK. og angis alltid med tre sifre, f.eks. B = 045°. Avstanden til A fra fartøyet angis i nautiske mil. Den korteste veien mellom to punkter på en kuleoverflate er alltid en del av en storsirkel. En storsirkel er en sirkel på jordkuleoverflaten hvor sirkelens sentrum ligger i kulas sentrum. (Ill.: H. Fjeld 1985)
Når vi plasserer polarkoordinatsystemet slik at fartøyet ligger i origo og 0-linjen ligger etter meridianens nordretning, kan vi bestemme et punkts plassering i forhold til fartøyet. Vinkelen B kalles rettvisende peiling og angis alltid med tre sifre, f.eks. B = 045°. Avstanden til A fra fartøyet angis i nautiske mil. Peilelinjen mellom øyet i origo og objektet i punktet A er egentlig en storsirkel, og vinkelen mellom meridianens nordretning og punktet A en sfærisk vinkel, men siden avstanden innenfor synsfeltet er relativt liten, håndterer vi storsirkelen som en loksodrom og de observerte vinklene som plane. Loksodrom og sfærisk vinkel kommer vi tilbake til.
Dersom ingen forstyrrende krefter påvirker fartøyet, vil det forflytte seg fremover i langskipsretningen. Vinkelen mellom meridianen gjennom fartøyet og storsirkelen kalles fartøyets rettvisende kurs og betegnes Rv k, eller RK.
Forandret bredde og lengde, middelbredde og avvikning
Under en seilas seiler vi fra avfarende plass (avf pl) og til påkommende plass (påk pl). Når det gjelder bredde- og lengdekoordinatene, seiler vi fra avfarende bredde (avf br) og lengde (avf lgd), til påkommende bredde (påk br) og lengde (påk lgd).
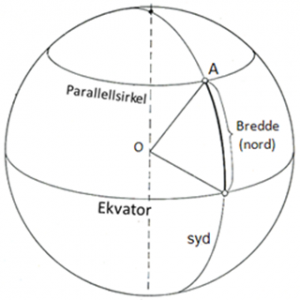
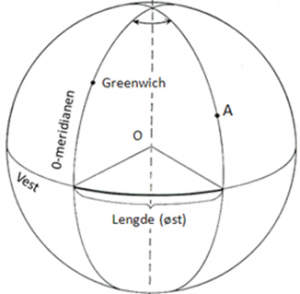
Fig. t.v.: Bredden til pkt. A er gitt ved vinkelen langs meridianen fra ekvator til stedets parallellsirkel. Fig. t.h.: Lengden til pkt. A er gitt ved vinkelen mellom nullmeridianen (Greenwich) og stedets meridian. Posisjonen er dermed gitt som et vinkelmål i forhold til jordas sentrum.
Fra fig. t.v. ser vi at breddegraden til pkt. A er gitt ved vinkelen langs meridianen fra ekvator til stedets parallellsirkel. Posisjonen er dermed gitt som et vinkelmål i forhold til jordas sentrum. Vinkelen er mellom 0° – 90° nord for ekvator, nordlig bredde, eller syd for ekvator, sydlig bredde. Vanlige forkortelser for breddegrad er br, lat (for latitude), eller φ. Fra fig. t.h. ser vi at lengdegraden defineres av meridianene med referanse til 0-meridianen. Når vi beskriver lengdegraden til et sted kalles denne gjerne stedets meridian, og lengdegradene blir oppgitt som en vinkel vest eller øst for Greenwich. Posisjonen er også her gitt som et vinkelmål i forhold til jordas sentrum. Vestlig lengde går fra 0-meridianen og 180° vestover, mens østlig lengde går 180° østover. Vanlige forkortelser for lengdegrad er lgd, long (for longitude), eller λ.
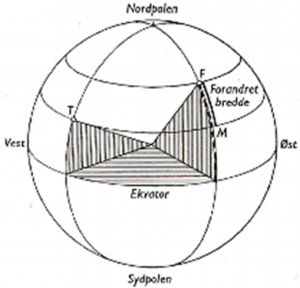
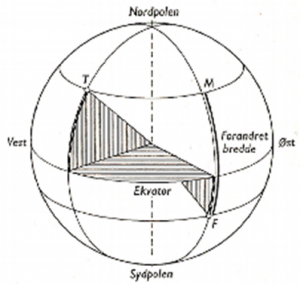
Fig. t.v.: Forandret bredde er stvkket FM. Den er forskjellen mellom F og T’s bredde. Hvis seilasen går fra T til F er forandret bredde nord (N). Hvis seilasen går fra F til T er forandret bredde sør (S). Fig t.h.: Forandret bredde er stykket FM. Den er summen av F og T’s bredde.
Hvis F og T ligger på hver sin side av ekvator, er forandret bredde lik summen av breddene.
Forandret bredde
Forandret bredde (f br, bf eller Δbr) under en seilas er breddeforskjellen mellom avfarende bredde (avf br) og påkommende bredde (påk br). Som en definisjon kan vi si at forandret bredde, breddeforskjellen mellom to steder, er lik stykket av en meridian mellom de to stedenes parallellsirkIer, vanligvis målt i buegrader. For avfarende og påkommende bredde på samme side av ekvator, er forandret bredde lik forskjellen mellom breddene. For avfarende og påkommende bredde på hver sin side av ekvator, er forandret bredde lik summen av breddene. Forandret bredde benevnes nord (N) når vi seiler nordover, sør (S) når vi seiler sørover.
Eksempel 3 – se fig. over t.v.
Vi seiler fra F til T og skal finne forandret bredde. F’s bredde er N 60o 27’ og T’s bredde er
N 24o 15’. Vi stiller opp slik:
avf br N 60° 27’
påk br N 24° 15’
f br S 36° 12’
For to steder på samme side av ekvator, er forandret bredde lik forskjellen mellom breddene. Forandret bredde benevnes sør når vi seiler sørover.
Eksempel 4 – se fig. over t.h.
Vi seiler også her fra F til T. Avf og påk pl ligger nå på hver sin side av ekvator. F’s bredde er S 19o 27’ og T’s bredde er N 40o 19’. Vi stiller opp slik:
avf br S 19° 27’
påk br N 40° 19’
f br N 59° 46’
Dersom stedene ligger på hver sin side av ekvator, er forandret bredde lik summen av breddene. Forandret bredde benevnes nord når vi seiler nordover.
Middelbredden
Parallellsirkelen som ligger midt mellom avfarende og påkommende bredde, kalles middelparallellen. Som en definisjon kan vi si at middelbredden (m br eller bm) er stykket av en meridian fra ekvator til middelparallellen målt i buegrader. Middelbredden har betydning for beregninger når vi senere skal seile middelbreddeseilas. For avfarende og påkommende bredde på samme side av ekvator, finner vi middelbredden ved å legge dem sammen og dividerer summen med 2.
Eksempel 5
avf br N 51° 18′
påk br N 49° 50′
sum 101° 08′
m br N 50° 34′
For avfarende og påkommende bredde på hver sin side av ekvator, trekker vi dem fra hverandre og dividerer forskjellen med 2.
Eksempel 6
avf br S 00° 51’
påk br N 01° 53′
differanse 01° 02′
m br N 00° 31′
Forandret lengde
Forandret lengde (f lgd, lf eller Δlgd) under en seilas er lengdeforskjellen mellom avfarende lengde (avf lgd) og påkommende lengde (påk lgd). Som en definisjon kan vi si at forandret lengde er lengdeforskjellen mellom to steder, eller stykket av ekvator mellom de to stedenes
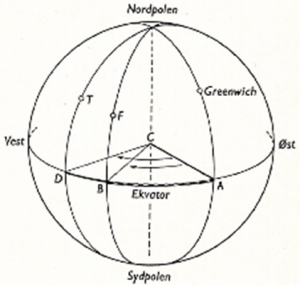Her er T’s lengde lik stykket AD. F’s lengde er stykket AB. Forandret lengde er stykket DB om vi seiler østover, eller BD, om vi seiler vestover. (Ill.: H. Fjeld 1985)
meridianer, vanligvis målt i buegrader. Er avf lgd på østlig halvkule og påk lgd på vestlig finner vi forandret lengde ved å legge lengdene sammen. Vi regner alltid korteste vei, W eller E, og blir summen over 180° må vi trekke denne fra 360° for å få den riktige lengdeforandringen. Er begge stedene på øst eller vest lengde, får vi forandret lengde ved å trekke dem fra hverandre. Forandret lengde er øst når vi seiler østover og vest når vi seiler vestover, uansett om vi befinner oss på den vestlige eller østlige halvkule.
Eksempel 7 – fig. over
Vi seiler fra T til F og vil bestemme forandret lengde. Både T og F ligger vestenfor Greenwich, og vi må trekke dem fra hverandre. Vi stiller opp slik:
avf lgd W 60° 15’
påk lgd W 35° 10’
f lgd E 25° 05’
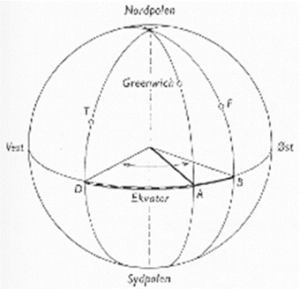Her er T’s lengde lik stykket AD. F’s lengde er stykket AB. Forandret lengde er stykket DB eller BD, avhengig av om vi seiler østover eller vestover. (Ill.: H. Fjeld 1985)
Eksempel 8 – fig. over
Vi seiler fra T til F og vil bestemme forandret lengde. Nå ligger T og F på hver sin side av Greenwich (0-meridianen) og vi må legge lengdene sammen. Vi stiller opp slik:
avf lgd W 45° 10’
påk lgd E 25° 15’
f lgd E 70° 25’
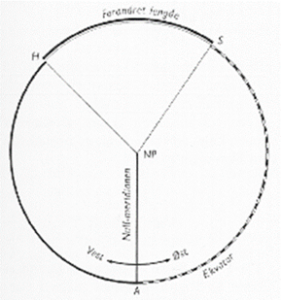Her er jorda sett over nordpolen. A er nullmeridianen, H er Honolulu og S er Sydney. Honolulus lengde W er stykket AH, og Sydneys lengde E er stykket AS. Forandret lengde er stykket SH eller HS, avhengig av om vi seiler østover eller vestover. Vi regner alltid forandret lengde den korteste veien. (Ill.: H. Fjeld 1985)
Eksempel 9 – fig. over
Vi seiler fra Sydney (S) til Honolulu (H) og vil finne forandret lengde. Både S og H ligger på hver sin side av Greenwich (0-meridianen) og vi må legge lengdene sammen. Vi regner alltid forandret lengde den korteste veien. Summen av lengdene blir mer enn 180° og vi må trekke fra 360°. Honolulu ligger østenfor Sydney, og forandret lengde blir øst. Vi stiller opp slik:
avf lgd E 15 1° 13’
påk lgd W 157° 52’
sum 309° 05’
f lgd E 50° 55’
Eksempel 10
Finn påkommende lengde (Påk lgd):
Rv kurs Distanse Avf lgd Avf br
E 59,0 n.mil W 015°12’ N 49°40’
Svar: lf = 59,0 / cos 49°40′ = 91,2′ = 1°31’
Avf lgd W 015° 12’
lf E 1° 31’
Påk lgd W 013° 41’
Avvikning
Avstanden mellom to meridianer, målt i nautiske mil, kalles avvikning (avv). Fig. under viser sammenhengen mellom avvikning og forandret lengde på forskjellige bredder. Forandret lengde er den samme på parallellsirklene fra ekvator til polen, mens avvikningen – den fysiske lengden målt i nautiske mil – blir mindre og mindre etter hvert som bredden øker. På ekvator er avv, målt i nautiske mil, lik forandret lengde i bueminutter. På 60° bredde har avstanden mellom de to meridianene avtatt til halvparten av hva den var på ekvator. Ved seilas kaller vi det antall nautiske mil som vi kommer fram i rettvisende 090° eller 270° for avvikning. Vi kan gjøre avv om til forandret lengde og forandret lengde om til avv ved trigonometrisk beregning.
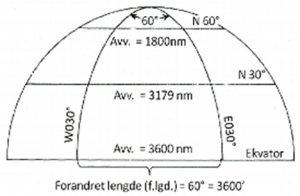
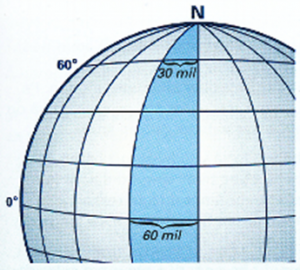Sammenhengen mellom forandret lengde og avvikning på forskjellige bredder.
På 60° bredde (N og S) er den fysiske avstanden mellom lengdegradene halvert i forhold til ekvator, mens forandret lengde er den samme. En parallellsirkels omkrets er lik ekvators omkrets multiplisert med cosinus til parallellsirkelens bredde. Cosinus til parallellsirkelens bredde 60° er 0,5. Ved polene ligger lengdegradene tett i tett før de samles i selve polpunktet. (Ill.: S. Løken 2008)
Vi kaller ekvators omkrets for E og dens radius for R, parallellsirkelens omkrets for P, og dens radius for r, og setter følgende proporsjon:
E : P = 2πR : 2πr Vi forkorter og får E : P = R : r
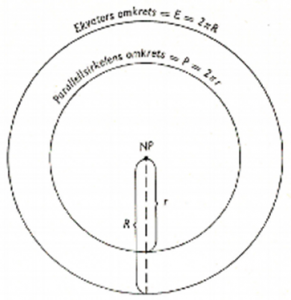Jorda sett over nordpolen. E = ekvators omkrets, P = en vilkårlig parallellsirkels omkrets,
R = ekvators radius og r = parallellsirkelens radius. (Ill.: H. Fjeld 1985)
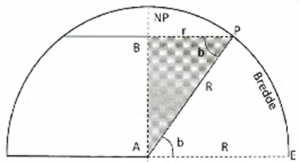R er jordkulas radius, r er parallellsirklenes radius, og b er parallellsirkelens bredde. (Ill.: H. Fjeld 1985)
Av dette følger: 1) E = P • R/r = P • 1/r/R som gir 2) P = E • r/R
Vi ser av fig. over at r/R = cos bredden. Vi setter inn i ligning 1) og 2) og får
1) E = P/cos br og 2) P = E • cos br
Definisjonen blir slik:
Ekvators omkrets er lik en parallellsirkels omkrets dividert med cosinus til parallellsirkelens bredde, og –en parallellsirkels omkrets er lik ekvators omkrets multiplisert med cosinus til parallellsirkelens bredde.
Det som er vist for hele sirkelen, gjelder også for deler av den. Et stykke av ekvator er forandret lengde, og et stykke av en parallellsirkel er avvikning. Når vi måler forandret lengde i bueminutter, kan vi si det slik:
- lgd. = avv : cos parallellsirkelens bredde
avv = f lgd • cos parallellsirkelens bredde
Når vi vil se nærmere på forholdet mellom polare og kartesiske koordinater, bruker vi en fig. som kanskje enklere viser oss at r/R = cos bredden. Vinkelen θ angir breddegraden til parallellsirkelen, hosliggende katet (r cos θ) er parallellsirkelens radius, og hypotenusen r er jordkulas radius.
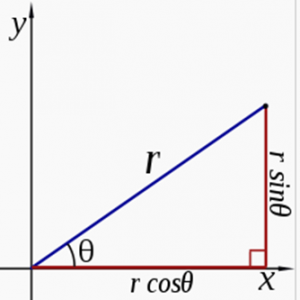Figuren viser forholdet mellom polare og kartesiske koordinater.
Fart, tid og distanse
Buemål og tidsmål er viktig i navigasjon. Soldøgnet varierer fra vel 23 timer og 59 minutter til snaut 24 timer og 1 minutt. Gjennomsnittsdøgnet på 24 timer danner utgangspunktet for tidsregningen. Hvis vi tenker oss en middelsol som går rundt jorda i ekvatorplanet med jevn hastighet, 360° på 24 timer uten avvik, kan vi lage tabell over sammenhengen mellom tidsregning og buemål.
Distansen er den avstanden et skip tilbakelegger i en gitt tid. Distansen måler vi i nautiske mil. Skipets fart angis i knop, hvor en knop betyr en nautisk mil tilbakelagt pr. time. Et skip
som gjør 15 knop, har en fart av l5 nautiske mil pr. time. Distansen finner vi ved å multiplisere farten i knop med tiden i timer. Et skip som gjør 15 knop, har en utseilt distanse på 150 n mil på l0 timer.
Tabell over sammenhengen mellom tidsregning og buemål.
Når vi regner fart, tid og distanse kan mange ha nytte av den såkalte fartstrekanten.
Distansen (D) i n mil finner vi ved å multiplisere farten (F) i knop med tiden (T) i timer.
Tiden (T) i timer finner vi ved å dividere distansen (D) i n mil med farten (F) i knop.
Farten (F) i knop finner vi ved å dividere distansen (D) i n mil med tiden (T) i time.
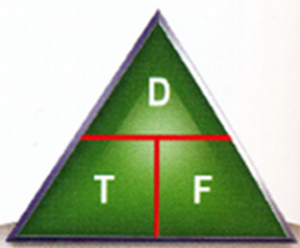Mange kan ha nytte av den såkalte fartstrekanten.
Begrepet knop
En knop = en nm/t = 1,852 km/t = 0,514 m/s. Selve begrepet knop (knute) kommer opprinnelig fra den tiden hastigheten ble målt med en loggline som var merket med knuter med like stor avstand i mellom. Når vi gjør om en knop til m/min får vi:
1852 m : 60 min = 30,87 m/min
Hvis avstanden mellom knutene på logglinen var 30,87 m, var det bare å telle antall knuter i løpet av ett minutt etter hvert som logglinen gikk ut. I tidligere tider ble tiden målt med vannklokke, og senere med timeglass.
Fartsmil
I dag måler vi skipets hastighet med satellittbaserte systemer som gir stor grad av nøyaktighet. Når man tidligere ville sjekke en logg, eller måle skipets hastighet nøyaktig, var det vanlig å gå en fartsmil. Dette er en nøyaktig oppmålt distanse på en nautisk mil (1852 meter) som er merket langs en strandlinje, gjerne med overettmerker ved start og slutt. Distansen ble seilt begge veier og hastigheten ble beregnet.
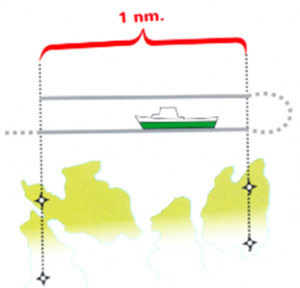Eksempel på fartsmil med overettmerker ved sta dsbåtskipperen, rt og slutt. (Fra Fritidsbåtskipperen, Gyldendal, 2008)
Eksempel 11
Vestgående seiler vi i 160 sekunder, og østgående seiler vi i 180 sekunder. Hva blir skipets fart i knop gjennom vannet? Gjennomsnittstiden blir da 170 sekunder (s).
Svar: Skipets fart gjennom vannet (v) blir:
v = 3600 s / 170 s = 21,2 kn
Logaritmisk fart/tid-skala
Når du regner med fart, tid og distanse, må du som regel gjøre om timer til minutter. Da kan det være greit å bruke den logaritmiske fart/tid-skalaen. Den er gjengitt i en del kartpublikasjoner, og bl.a. nederst på maneuvering board-arkene, se fig. Her kan du beregne farten når du kjenner tiden og distansen, tiden når du kjenner distansen og farten, og distansen når du kjenner farten og tiden.
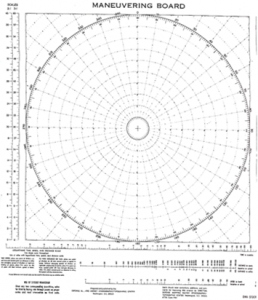Den logaritmiske fart/tid-skalaen er gjengitt bl.a. nederst på maneuvering board-arkene.
Finn farten
Du har seilt 5 nautiske mil på 23 minutter og ønsker å finne gjennomsnittshastigheten. Du setter den ene passerspissen i (5) på skalaen, og den andre i (23). Så flytter du det ene passerbenet til 60, og hvis du nå har klart å beholde vinkelen, skal det andre da havne i 13 (knop) – som er farten i dette tilfellet.
Finn tiden
Du lurer på hvor lang tid du vil bruke på 6,5 n. mil hvis farten er 5 knop. Du starter også nå med distansen (6,5). Så setter du den andre passerspissen i farten (5). Siden skalaen her ikke går lenger enn til 60, flytter du passerbenet til 6 (i stedet for til 60) og leser av 7,8 – altså 78, som blir tiden i minutter, dvs 1 time og 18 minutter.
Finn distansen
Du ønsker å finne ut hvor langt du kommer på 40 minutter med en fart på 12 knop. Nå bruker du skalaen baklengs. Ta utgangspunkt i (60) og sett det andre passerbenet i (12). Så forflytter du det ene benet til 40 og leser av 8 (n. mil) ved det andre.
Eksempel 12
Hva blir utseilt distanse fra kl. 1100 til kl. 1445 når farten er l4 knop?
Distansen (D) i n mil finner vi ved å multiplisere farten (F) i knop med tiden (T) i timer.
Svar: Intervall fra kl. 1100 til kl. 1445 = 3 h 45 min = 3,75 timer
14 kn · 3,75 t = 52,5 n mil. Utseilt distanse blir 52,5 n mil
Eksempel 13
Hva blir farten hvis fartøyet tilbakelegger 0,7 n mil på 2 min?
Farten (F) i knop finner vi ved å dividere distansen (D) i n mil med tiden (T) i timer.
Svar: 0,7 n mil dividert på 2 min = 0,35 n mil på ett min. For å få kn pr t må vi multiplisere med 60 min = 0,35 n mil x 6o min = 21 kn Farten blir 21 kn
Eksempel 14
Når regner du med å komme fram til bestemmelsesstedet (ETA = Estimated time of arrival) dersom distansen dit er 33,25 n. mil, fartøyets hastighet er 9,5 knop og seilasen starter kl 1100? (ETD = Estimated time of departure).
Tiden (T) i timer finner vi ved å dividere distansen (D) i n mil med farten (F) i knop.
Svar: Tid å seile = 33,25 n. mil : 9,5 knop = 3,5 timer, dvs. 3 h 30 min
ETD 1 100
Tid å seile 0330
ETA 1430
Eksempel 15
Fartøyet ditt har følgende farts- og manøvreringskarakteristikk:
Full Ahead: 18 knop
Half Ahead: 13 knop
Slow Ahead: 10 knop
Dead Slow Ahead: 7 knop
Det er midnatt og dere skal ta los kl 0400. Det er 50 n.mil igjen til losstasjonen og skipets fart er 18 knop (Full Ahead). I nattordreboken har kapteinen skrevet at dere skal holde Full Ahead inntil nødvendig restfart tilsvarer Slow Ahead. Da skal maskinen bemannes og dere skal begynne å redusere farten. Hvor lenge er det til restfarten er 10 knop og dere må begynne å redusere gitt at farten holder seg på 18 knop inntil videre?
Svar: x = antall timer med 18 knop, y = antall timer med 10 knop
x + y = 4 => x = 4 – y
18x + 10y = 50 => 18(4 – y) + 10y = 50
72 – 18y + 10y = 50 => 22 = 8y => y = 2.75
x = 4 – y => x = 4 – 2.75 = 1.25 timer
Det er 1.25 timer til farten må reduseres – altså kl 0115