3.0 Bølger

Fig. 3.01 Her ser vi Kelvins bølgemønster med veldefinerte side- og hekkbølger (Foto: Øystein Johnsen)
3.1 Bølger i sin alminnelighet
Siden oppgaven omhandler dynamiske problemer som følge av ulike typer belastninger i bølger på dypt vann, vil jeg her konsentrere meg om den delen av bølgeteorien som jeg mener er nødvendig for å kunne se den videre sammenhengen.

Fig. 3.02 Vinden forårsaker kappilarbølger og gravitasjonsbølger. (Trujillo og Thurman 2005)
Det finnes en rekke forskjellige typer bølger som kan forplante seg i en væske. Jeg vil her bare ta for meg overflatebølger da det er disse som har størst innvirkning på skipets stabilitet.
Vinden er den viktigste årsak til bølgedannelse.. En svak vind (mindre enn to knop) vil sette opp små bølger som kalles krusning eller kappilarbølger. Disse bølgene henger nøye sammen med overflatespenningen i vannet. Det er typisk for disse bølgene at de dør ut straks vinden forsvinner, og at bølger med liten bølgelengde beveger seg fortere enn dem med større bølgelengde, i motsetning til de bølger som heretter vil bli omtalt.
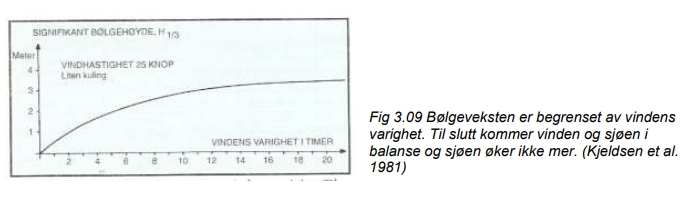
Ved sterkere vind oppstår overflatebølger (også kalt gravitasjonsbølger). Bølgene mottar energi fra vinden inntil en viss likevekt er oppnådd. Viktige faktorer her er vindens styrke, vindens stabilitet med hensyn til både retning og fart, og størrelsen på det området vinden virker på (fetch). Selve energioverføringen fra vind til bølge skjer ved trykkpulser og friksjonskrefter. Etter at bølgene er dannet, kan de bevege seg over store havområder (energikonservering). Senere vil de gradvis brytes ned ved interferens, refraksjon, brytning og friksjonskrefter.
På samme måten som vinden kan danne bølger, kan vinden også dempe ned bølger. Man er kjent med at en temmelig opprørt sjø kan dempes effektivt i løpet av noen få timer ved vindens virkning. (Torsethaugen 1998)
3.11 Masse og momentum bevares under bevegelsen
Når en iakttar et opprørt hav virker det kaotisk, som om det ikke finnes noen orden og lovmessighet der. Men det er bare tilsynelatende. Selv om bevegelsen av en væske har uendelig mange frihetsgrader
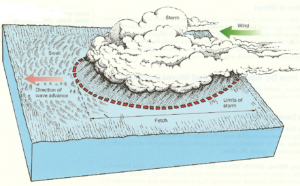 Fig. 3.03 «The Sea and Swell». (Trujillo og Thurman 2005)
Fig. 3.03 «The Sea and Swell». (Trujillo og Thurman 2005)
(med antall frihetsgrader menes det antall forskyvningsparametre vi har til rådighet når bevegelsen skal beskrives) er den likevel bestemt av dynamiske lover. Disse uttrykker at masse og momentum bevares under bevegelsen, og er formulert i et matematisk språk (partielle differensialligninger). Det finnes selvsagt en uendelighet av mulige bevegelser.
(Momentum = Masse ● Hastighet(kg ● m/s)) ikke til forveksling med
(Moment = Masse ● Arm(kg ● m))
3.12 Det er ikke en vannmengde som beveger seg.
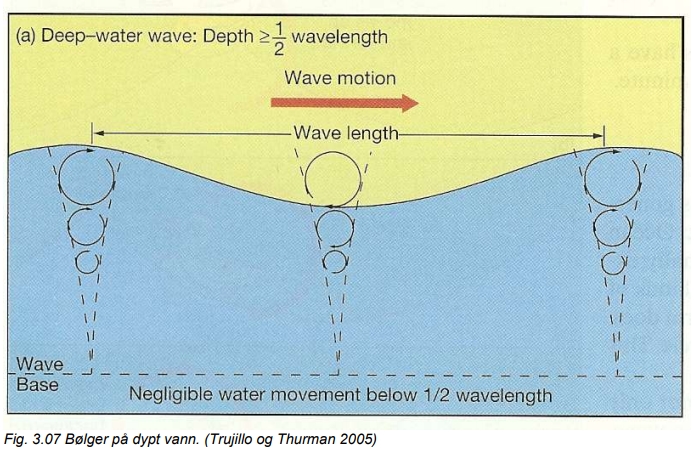
Når en bølge beveger seg framover, er det ikke en vannmengde som beveger seg. Det er bølgeformen som forplanter seg bortover vannflaten. Vannpartiklene beveger seg bare opp og ned og fram og tilbake. Dette kan vi se av f.eks. en kork som flyter på vannet, den vil bare løftes og senkes og flyttes litt fram og tilbake når en bølge passerer. I en bølge er toppene spissere enn bølgedalene. Dette henger sammen med måten bølgene blir dannet på. Det viser seg at vannet i bølgen i virkeligheten
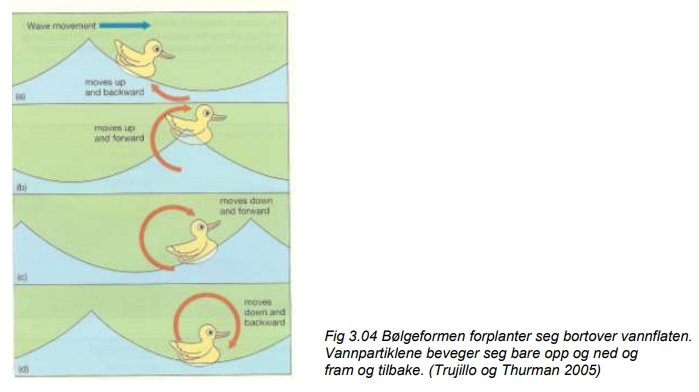
beveger seg i vertikale sirkler, som nær overflaten har en diameter lik bølgehøyden. I en bølgetopp beveger vannet seg i samme retning som bølgen, og i en bølgedal beveger vannet seg i motsatt retning.
3.13 Bølgelengde, bølgehøyde og bølgeperiode.
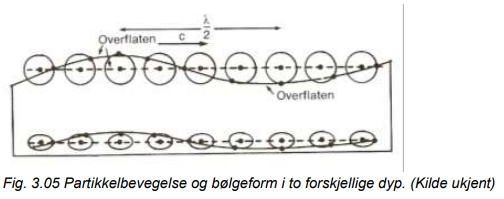
Fig. 3.05 viser en enkel bølge. Avstanden mellom to bølgetopper kalles bølgelengden ![]() og den vertikale avstanden fra bølgetopp til bølgedal kalles bølgehøyden H. Bølgen i fig. 3.05 beveger seg fra venstre mot høyre, og tiden det tar for en bølgetopp å forplante seg en bølgelengde fram, kalles bølgens periode T.
og den vertikale avstanden fra bølgetopp til bølgedal kalles bølgehøyden H. Bølgen i fig. 3.05 beveger seg fra venstre mot høyre, og tiden det tar for en bølgetopp å forplante seg en bølgelengde fram, kalles bølgens periode T.
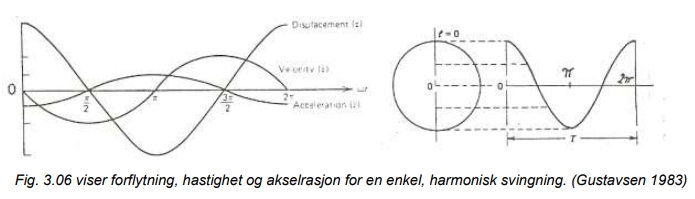
Av fig. 3.06 ser vi at perioden (3.01)
Dermed har vi vinkelfrekvensen gitt ved (3.02)
3.14 Fasehastighet (bølgefart, eller bølgens forplantnings-hastighet).
Bølgen forplanter seg med en hastighet som kalles fasehastighet (eller c). Fasehastigheten er altså den hastighet som bølgen som helhet beveger seg med. Bølgelengden dividert med perioden er lik fasehastigheten,
. Vi har
(3.02) og henter
(3.06) og
(3.07) og får da
. Når dybden er større enn en halv bølgelengde, er det minimal påvirkning fra bunnen. Fasehastigheten kan da beregnes til:
(3.03)
Vi har for alle bølger at der T er perioden. Dette gir
eller
.
En periode på 10 sek. gir da en hastighet på 15,6 m/sek og en bølgelengde på 156 m.
Vi ser at fasehastigheten er proporsjonal med kvadratroten av bølgelengden. Dette viser at lange bølger går raskere enn korte. Hvis havdybden er liten i forhold til bølgelengden (ca. 1/20), må hastigheten beregnes av:
(3.04)
der D er havdybden i meter. (Breen 1980). Fasehastigheten for de større bølgene ligger vanligvis på 70-85% av vindstyrken. Etter at vinden har stått en stund, vil det også oppstå enkelte lengre bølger som går hurtigere enn vinden. (Dannevig 1996)
3.15 Perioden i sekunder multiplisert med 3 gir bølgens fart i knop.
På dypt vann er den farten som bølgen går med bare avhengig av bølgeperioden. Vi har da den enkle regel at perioden i sekunder multiplisert med 3 gir bølgens fart i knop. Er f.eks. bølgeperioden 5 sekunder, går bølgen med en fart på 15 knop. (Breen 1980) Når vinden blåser, vil de største bølgene ha de lengste periodene, og disse går derfor fortest. Dette fenomenet kalles dispersjon (tilsvarende har en ved lysgjennomgang i et prisme). På grunt vann vil bølgene bare i liten utstrekning vise dispersjon. Dispersjonen er årsak til at dønningen i forbindelse med uvær ofte når kysten først og gir varsel om uvær til havs.
Størrelsen på bølgene, lengden og høyden, er altså bestemt av vindstyrken, hvor lenge vinden har stått på og lengden på det åpne havstrekket vinden blåser over.
3.16 Grensen for fasehastigheten er omkring 1,4 ganger vindhastigheten.
I passatstrøkene har vi svært stabile vindforhold, og her har en målt hastigheten av de fremtredende bølgene og sammenlignet med vindstyrken. Bølgene kan her gå med en fart på 20 knop, mens vindstyrken sjelden er over 16 knop. At bølgefarten er større enn vindhastigheten henger sammen med at vinden kan øve et effektivt drag på vannflaten selv om bølgen går fortere enn vinden. Det er bare bølgeformen som går fort, vannet selv som draget virker på, beveger seg langsomt. Der virkningen av dette draget blir opphevet av virkningen fra bremsingen, må grensen for bølgehastigheten ligge. Beregninger og observasjoner viser at grensen for bølgehastigheten er omkring 1,4 ganger vindhastigheten. (Breen 1980)
3.17 Bølgemønsterets hastighet (eller gruppehastigheten V).
De enkelte bølgers fasehastighet må ikke forveksles med den hastighet som bølgemønstret erobrer havflaten med. Den er halvparten så stor. Som et overslag kan vi regne med at denne gruppehastigheten i knop er lik perioden i sekunder multiplisert med 1,5. Fullt utviklede stormbølger kan ha perioder varierende mellom 7 og 24 sek. Vi får altså en utbredelseshastighet fra 10 til 36 knop. (Dannevig 1996)
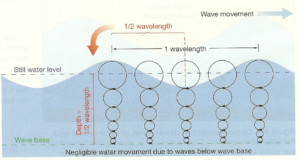
Fig. 3.08 Partikkelbevegelse. Bevegelsesmønsteret i bølgepartiklene strekker seg til en dybde av en halv bølgelengde, fra «flatt vann» (Still water level) som er bølgebevegelsens utgangspunkt. (Trujillo og Thurman 2005)
3.18 Vannpartiklenes hastighet.
Vannpartiklenes hastighet er ikke det samme som bølgens fasehastighet. På dypt vann vil vannpartiklene bevege seg i sirkler så lenge en ikke er nær bunnen. Når bølgen kommer inn over grunnere vann, deformeres sirkelbanene til ellipser. Hva som er grunt og dypt i denne forbindelse avhenger av bølgelengden i forhold til dybden. En snakker om bølgens evne til å «føle» bunnen. På dyp større enn bølgens halve bølgelengde vil bølgen ikke kunne «føle» bunnen. (Kjeldsen et al. 1981)
3.19 Signifikant bølgehøyde.
Middelverdien av den tredjedelen av bølgene som er høyest i et gitt tidsrom (ofte angitt som 20 min.), eller (standardavviket) til havoverflaten, kalles signifikant bølgehøyde.
Den høyeste bølgen en kan vente over tid, kan være 1.5 til inntil 2 ganger høyere enn signifikant bølgehøyde. Man har tidligere beregnet seg fram statistisk til en faktor på 1,86. (Gustavsen 1983)

3.2 Bølgen bryter.

Fig. 3.11 Styrtbrenning i en ekstrembølge og noen grunnleggende definisjoner for den samme bølgen. (Foto: Fukumi Kuriyama)
3.21 Bølger og strøm
Bølgenes utbredelse påvirkes av strømforholdene. Strømmens innvirkning på bølgene avhenger ikke direkte av strømhastigheten, men av variasjoner i denne.

Fig. 3.12 Når strøm og bølger møtes? Field Express i grov sjø. (Foto: Peet Smit)
F.eks., når bølger kommer inn i et område med økende motstrøm, vil bølgelengden avta og bølgehøyden øke – bølgene blir krappere. I motsatt fall, dersom bølgene kommer inn i et område med økende medstrøm vil bølgelengden øke og bølgehøyden avta – bølgene blir slakere. Strømmens innvirkning på bølgene avhenger av strømfarten og bølgeperioden (strømmen har størst innvirkning på bølger med lav bølgeperiode).

Fig. 3.13 Minste strømfart som stopper en bølge (med gitt bølgeperiode). (Torsethaugen 1998)
Dersom strømmen er sterk nok kan bølger som kommer inn i et område med økende motstrøm, bli fullstendig stoppet av strømmen. Fig. 3.13 viser hvilken strømfart som må til for å stoppe en bølge (med en gitt bølgeperiode). Når strømmen er sterkere enn dette, stoppes bølgene. Det vil si at bølgene blir så krappe at de bryter og mister sin energi. Resultatet vil ofte være at bølgene bryter som farlige styrtbrenninger. (Eks. Pentland o.l. Kalles ofte vannstandsprang).
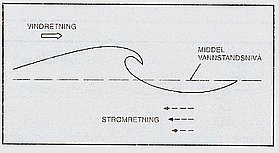
Fig 3.14 Svære brottsjøer kan dannes på steder hvor strøm og bølger går med motsatte retninger. (Sjøkartverket 1997)
Variasjoner i strømhastigheten gjør at bølgeretningen kan endres. Dette fenomenet kalles strømrefraksjon. I praksis er det vanskelig å forutsi eller beregne hvilken betydning strømrefraksjon har for bølgeforholdene i et område. Dette skyldes at det er nær umulig å oppnå en tilstrekkelig detaljert beskrivelse av strømforholdene for å kunne utføre slike beregninger. Strømskjær i stor målestokk er typisk de strømvirvler som beveger seg nordover langs Norskekysten. De vil forandre bølgenes retning ved refraksjon på samme måte som forandringer i dybde.
3.22 Bølgefrontens steilhet (eller krapphet).
Et annet viktig forhold ved overflatebølger er bølgefrontens steilhet, vanligvis definert som:
(3.05)
hvor ka er et ubenevnt tall, og et mål for den maksimale helningen på overflaten. Modellforsøk og sjøforklaringer har vist at en enkelt steil bølge kan være årsak til å vippe et skip rundt, og dersom stabiliteten ikke er tilstrekkelig, vil skipet ikke rette seg opp. (Kjeldsen et al. 1981)
Bølgekrapphet er altså definert som forholdet mellom bølgehøyde og bølgelengde. Bølgene blir følgelig krappere både som følge av at bølgehøyden øker og at bølgelengden avtar. Bølgekrappheten øker når dybden avtar. For moderate dybder øker bølgekrappheten som følge av at bølgelengden avtar.
Når dybden blir mindre enn 10 meter øker krappheten også som følge av at bølgehøyden øker. Dette betegnes vanligvis som grunning. F.eks., når bølger med periode på 12 sekunder kommer inn på 10 meter dybde, vil krappheten være nær det doble av krappheten på dypt vann: Dette skyldes en halvering av bølgelengden. Bølgehøyden vil i dette tilfelle være redusert med rundt 10 %.
Når bølger kommer inn i et område med sterk strøm, vil krappheten øke i motstrøm og avta i medstrøm. Bølgekrappheten er størst for bølger med liten bølgeperiode (korte bølger) og avtar når bølgeperioden øker. Generelt kan man si at bølger og sterk motgående strøm, dvs. strømfart større enn 0.5 m/s (1 knop), gir vanskelige bølgeforhold for mindre fartøy. (Torsethaugen 1998)

Fig. 3.15 Bølgekarakteristikker. (Trujillo og Thurman 2005)
3.23 Bølgen bryter
Erfaring viser at en bølge bryter når forholdet mellom bølgehøyde og bølgelengde overstiger forholdet 1:7 (2.02). Det viser seg også at en bølge bryter når forholdet mellom bølgehøyde og havdybde er mellom 0,6 og 0,8, altså mellom 3/5 og 4/5. Når bølgene kommer inn på grunt vann, vil bølgehøyden øke inntil bølgene blir så krappe at de bryter. Dette betyr at bølgebrytningen i det alt vesentlige er bestemt av dybden. Generelt kan man si at bølgene begynner å bryte når dybden blir mindre enn to ganger den signifikante bølgehøyden.
Bølger bryter også på dypt vann. Dette skyldes vekselvirkning mellom bølger av forskjellig periode og/eller retning. I praksis er det vanskelig å forutsi i hvilken grad bølgene kommer til å bryte på dypt vann. Bølgebrytning på dypt vann skjer langt sjeldnere enn på grunt vann.
Når bølger kommer inn i et område med økende motstrøm vil bølgelengden avta og de korteste bølgene (liten bølgeperiode) vil bli så krappe at de bryter. Dette omtales vanligvis som strømsjø. (Torsethaugen 1998)
3.24 Brytning av bølger på dypt vann / gruppedannelse
Når vannpartiklenes hastighet blir større enn bølgenes fasehastighet, opphører den regelmessige sirkelbevegelsen og bølgene bryter. Vannmassene beveger seg nå framover i bølgen. Denne bevegelse av vannmassene framover kan skje enten bare i bølgetoppen eller eventuelt over nesten hele bølgehøyden. Dette gir grunnlag for inndeling av bølgebrytningsfenomener i forskjellige typer. Her skal omtales to typer:
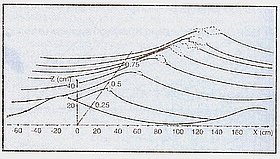
Fig 3.16 Observasjon av toppbrenning i laboratorieforsøk. Figuren viser hvordan brytningen utvikler seg over tid. (Sjøkartverket 1997)
Fig. 3.16 viser en toppbrenning i en dypvannsbølge når den bryter. Når bølgen oppnår maksimal steilhet, trekkes luft inn akkurat i toppen, og en blanding av luft og vann ruller ned over bølgens forside i små virvler.
Fig. 3.17 Observasjon av brottsjø i laboratorieforsøk. Brottsjøen dannes ved fokusering av all energien fra en bølgetopp. (Sjøkartverket 1997)
Fig. 3.17 viser en styrtbrenning i en dypvannsbølge. Styrtbrenning eller brottsjø er karakterisert ved at hele vannmassen velter forover og faller ned på bølgens forside. Herved dannes et omtrent sirkelformet område på bølgens forside hvor luft innesluttes. Denne brytningstype kan gi anledning til store støttrykk.
Flere brytningstyper vil kunne forekomme på dypt vann, men de to ovenfor angitte er de vanligste og det er egentlig ikke noe skarpt skille mellom disse typene. Vindens betydning for brytning av bølger bør også understrekes. Selv bølger med beskjeden bølgehøyde sammenlignet med bølgelengden, vil lett kunne bryte under påvirkning av vindkrefter.
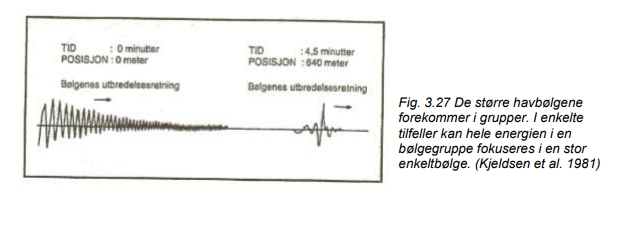
Det er kjent at havbølger opptrer i grupper hvor bølgehøyden og perioden varierer for hver enkeltbølge innenfor gruppen (fig. 3.18). Denne gruppedannelse kan være svært viktig for stabiliteten til et skip. Det kan således være av avgjørende betydning om et skip skal kunne klare en ekstrem bølge, eller to eller flere ekstreme bølger som følger rett etter hverandre, og muligvis rammer fartøyet flere ganger før det har rettet seg helt opp etter det første anslaget.

Fig. 3.18 Dannelse av stormbølger på dypt vann. Øverst ses en bølgegruppe dannet i et laboratorieforsøk, og nedenfor ses hvordan bølgegruppen utvikler seg på to senere tidspunkter. Man ser hvordan all bølgeenergien konsentreres i noen få eller en enkelt ekstrem bølge med stor høyde. (Kjeldsen og Myrhaug 1978).
Fig. 3.18 viser resultater fra et laboratorieforsøk hvor en bølgegruppe er dannet, og figuren viser hvorledes man til et senere tidspunkt observerer hvordan de enkelte bølgene går sammen, og at bølgeenergien konsentreres i en enkelt eller noen ganske få ekstreme bølger.
3.3 Havbølger

Fig. 3.19 Bølgetog under utvikling. (Trujillo og Thurman 2005)
3.31 Periodisk bølgetog
Når det gjelder å beskrive havbølger teoretisk er det enklest å ta utgangspunkt i et periodisk bølgetog. Det vil si en bølge som er periodisk både i rom og tid, med en bølgelengde λ , en periodetid T og en amplitude a. For en periodisk bølge blir da bølgehøyden H = 2a. I stedet for bølgelengde og periode kan det være hensiktsmessig å bruke størrelsene bølgetall k og frekvens ω gitt ved relasjonene (3.06) og (3.02):
(3.06)
og
(3.02)
Den første som studerte en slik bølge teoretisk var Franz Josef von Gerstner (1789-1823), professor i matematikk i Praha. I Teorie der Wellen fra 1802 fant han en eksakt periodisk løsning av de dynamiske ligningene for væsker med fri overflate. Fra denne løsningen fikk han sammenhengen mellom k og ω (eller λ og T) på den enkle formen:
(3.07)
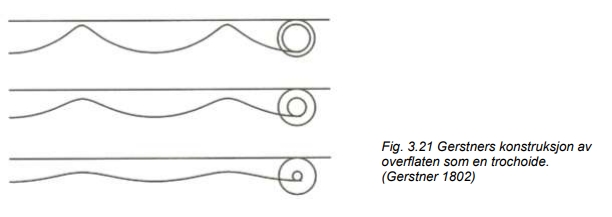
hvor g er tyngdens akselerasjon (g = 9,81 m/s2). Han fant at overflaten har form av en omsnudd trochoide. En trochoidekurve kan genereres av et punkt på en sirkulær skive som ruller uten å gli på et plant underlag, se fig. 3.21.

Fig. 3.20 Sammenligning av bølgeprofiler. (Gustavsen 1983)
Bølgelengden for trochoiden blir da lik omkretsen til skiven, derfor er skivens radius . Videre fant Gerstner at væskepartiklene utfører sirkulære bevegelser. Ved overflaten er radien i denne bevegelsen lik bølge-amplituden a, men den avtar fort (eksponensielt) nedover i væsken. En halv bølgelengde under overflaten er bevegelsen redusert med hele 96 %. Denne bølgemodellen viser seg å være korrekt når amplituden er mye mindre enn bølgelengden, ka << 1.
Størrelsen ka (ubenevnt tall), er relatert til bølgens steilhet og er et mål for den maksimale helningen på overflaten. For steilere bølger gir ikke Gerstners løsning noen god beskrivelse av det fysiske bølge-fenomenet. For små steilheter ka << 1, får en fra Gerstners løsning en sinus- eller cosinusfunksjon:
η = a cos(kχ − ωt) (3.08)
hvor η betegner hevningen av overflaten over likevektsnivået, og relasjonen (3.07) mellom k og ω er oppfylt. (Gerstner 1802)
3.32 Fouriers oppdagelse
Den franske matematiker og fysiker J.B. Fourier (1768-1830) utga i 1822 arbeidet Theorie Analytic de la Chaleur, hvor han påsto at enhver rimelig funksjon kunne skrives som en sum av sinus- og cosinusfunksjoner. Fouriers anvendelser av denne teorien var innen beregning av varmeledning. Men den egnet seg ypperlig til mange formål, både i matematikken og i anvendelser, også innen bølgeteorien.

Fig. 3.22 Eksempel på kryssende bølgetog. (Trujillo og Thurman 2005)
Det meste av den bølgeteorien som ble utviklet fram til første halvdel av det tyvende århundre begrenser seg til små steilheter, ka << 1. Så lenge denne steilheten er et lite tall (i praksis mindre enn 0,1) er de dynamiske ligningene tilnærmet lineære. Lineære ligninger er noe matematikere er glade i. De har nemlig den egenskapen at dersom A1 er en løsning og A2 en annen, så vil også A1 + A2 være en løsning.
Resultatet (3.08) har mer å si oss. Løsningen har to frie parametre a og k, i det ω er gitt som en funksjon av k via (3.07). Her må vi riktignok begrense oss til tilfellet ak << 1 for at (3.08) skal kunne brukes. Når de dynamiske ligningene er lineære, betyr det at vi kan bygge opp en vilkårlig løsning som en sum av elementære løsninger av typen (3.08), med amplitude an og bølgetall kn (n =1,2,3…).
![]()
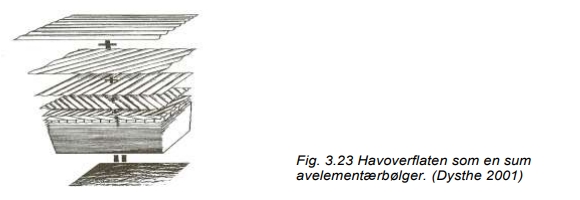
hvor θn er fasekonstanter. Videre er ωn = ω(kn) hvor sammenhengen mellom ω og k er gitt ved (3.07). Det overstående kan utvides til bølger som går i forskjellige retninger horisontalt. En kan nå benytte dette til å syntetisere en havoverflate med bølger som antydet på fig. 3.23.
Et enkelt spesialtilfelle av (3.09) gir innsikt i en viktig egenskap ved havbølgene. Vi ser på summen av to elementærbølger med samme amplitude, men med litt forskjellige bølgetall k og k + Δk. Dette gir:
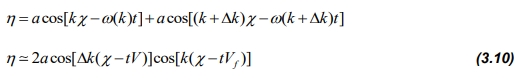
hvor størrelsen V kalles for gruppehastigheten og kan finnes fra (3.10) og (3.07) som (3.11):
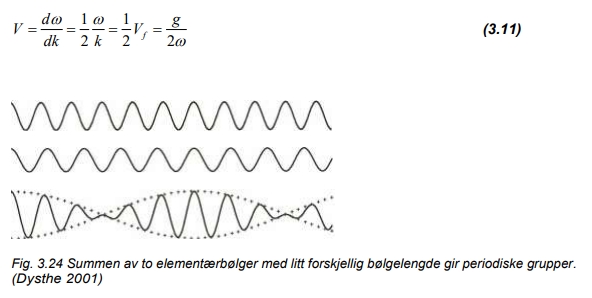
Fra uttrykket (3.10) og fig. 3.24 ser vi at denne kombinasjonen resulterer i periodiske grupper av bølger. (Dysthe 2001)
3.33 De to hastighetene
Fra eksemplet ovenfor er det klart at en har to forskjellige hastigheter:
(i) Fasehastigheten Vf = ω/k angir hvor fort bølgemønsteret forflytter seg (f.eks. farten til en bølgerygg).
(ii) Gruppehastigheten V angir hastigheten til en gruppe av bølger («omhyllningskurvene» i fig. 3.25).
Dette er den hastigheten som energien transporteres med. Fra (3.11) ser vi at V = Vf /2. Når en betrakter en gruppe av bølger, ser det ut som om bølgene skapes i bakkanten, for så å bevege seg framover og endelig forsvinne i gruppens forkant.
Bølgene egner seg ikke som informasjonsbærere slik som lydbølger og elektromagnetiske bølger. Ethvert endelig signal består av mange frekvens-komponenter. Da hver komponent går med sin egen hastighet (som er omvendt proporsjonal med frekvensen, se (3.11)), vil signalet fort bli forvrengt til det ugjenkjennelige. Det betyr ikke at bølgene er uten informasjonsverdi. Forstyrrelsen fra et stormsentrum i et verdenshav, bærer informasjon om hvor og når denne begivenheten fant sted, nemlig den informasjon som ligger i ankomsttiden til de forskjellige frekvenskomponentene. Den tiden τ det tar for bølger med frekvens ω å bevege seg fra kildeområdet til det stedet hvor vi observerer dem, blir τ = D/V = 2Dω/g hvor D er avstanden. Frekvensen ω blir da følgende funksjon av tiden:
ω = g/2D•T (3.12)
som sier at frekvensen øker proporsjonalt med transitt-tiden τ. Stormen som skapte bølgen er fjern både i tid og rom. En storm som fant sted 5000 km. ute på havet, vil skape store bølger som etter ca. 6 døgn når inn til kysten i form av dønninger.

I prinsippet kan en observatør som er utstyrt med stoppeklokke og papir, måle periodetiden til dønningene som skyller inn over stranden. Dersom en gjør dette periodisk over et par døgn, kan en finne ut når og hvor stormen herjet som verst, som antydet på fig. 3.25. (I praksis kan dette bli komplisert ved at dønning kan skrive seg fra mer enn ett stormområde.)
3.34 Steile bølger og ekstrembølger
Gerstners løsning er ikke anvendelig for steile bølger (ka > 0.1). Stokes (1847) derimot, klarte å finne relevante løsninger for periodiske bølger. Han fant at den teoretisk mest steile bølgen som kunne forekomme var når a/λ ≈1/14 , og denne hadde flate buker og hjørneaktige bølgekammer med en hjørnevinkel på 120°.
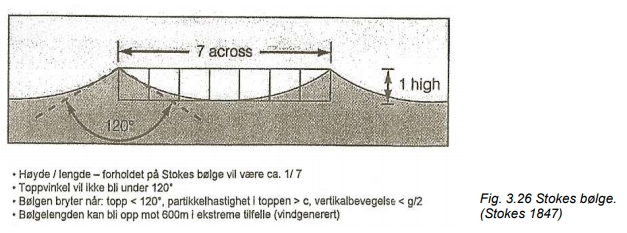
De lange stormbølgene som bærer det meste av bølgeenergien, er ikke spesielt steile. Den lineære teorien er derfor en rimelig bra tilnærming til mange formål. Det betyr ikke at de såkalt ikke-lineære effektene er uten betydning. Det innebærer at de forskjellige frekvenskomponentene som et opprørt hav består av ikke er uavhengige, men kan vekselvirke med hverandre. Selv om denne vekselvirkningen er svak, kan den forårsake kraftige effekter når den får virke over tid.
På midten av 1960 tallet kom det fart i forskningen på ikke-lineære bølgeeffekter. Det var starten på en blomstringstid for bølgeteorien med anvendelser bl.a. i akustikk, optikk og fluiddynamikk, med nye begreper som solitoner, parametrisk forsterkning, selvfokusering og selvmodulasjon. De siste årene har en vært spesielt opptatt av den innflytelse disse effektene kan ha på forekomsten av ekstreme bølger.
3.35 Dønning
Når et stormsentrum passerer et havområde, blir det opprørt hav og store bølger. Hvert vindkast vil sette opp grupper av bølger som forplanter seg ringformet utover. Det er bare de som går omtrent med vinden, som vil vokse. Slike nydannede bølger er svært krappe, og hvis bølgehøyden blir større enn en sjudel av bølgelengden, vil de bryte (2.02). Fra stormsenteret forplanter bølgene seg utover, og går over til regelmessige bølger. Sjøen «legger» seg ved at bølgelengden vokser på bekostning av høyden. Bølgene går over til dønning, som kan forplante seg over enorme strekninger. (Breen 1980) De mottar ingen energi fra vinden, den opparbeidede bevegelsen dempes gradvis ved indre friksjon i vannet. Alle småbølgene som har liten energi, dempes raskt, mens de lange bølgene kan rulle langt uten særlig reduksjon i høyde. Dønninger gir et ensartet bilde, havflaten kan følge en naturlig og regelmessig svingningstilstand. Vindpresset med alle de store brottene er borte. Dønningen har lave og avrundede, lange kammer. Serier av flere ganske høye dønninger følges av serier med forholdsvis lave. (Dannevig 1996)
Dønningen har så stor fart at den går fra uværssenteret, og på dønningen vil en ofte kunne forutsi at det er storm i vente. Stormbølger i Nord-Atlanteren er registrert som dønning i Sør-Atlanteren. Bølger innenfor et stormområde har sjelden en periode over 10 sek., og bølgelengden er da ca. 170 m. Som dønning har de en periode på mer enn 20 sek., og bølgelengden ligger på 800 – 1.000 m. Bølgehøyden kan være opp til én meter. (Breen 1980)

Fig. 3.28 Handelsfartøyet WINTER WATER i møte med den tropiske stormen Georgette. (NOAA Photo Library 1993).
Litteraturliste
Breen, O. (1980): Oseanografi.
Dannevig, P. (1997): Meteorologi og oseanografi for sjøfolk, 12. utg.
Dysthe, K.B. (2001): Matematisk modellering av havbølger.
Gerstner, F.J.v. (1802): Teorie der Wellen.
Gustavsen, J. (1983): Sikring og stuing av stykkgodslast. NTH.
Kjeldsen, S.P., Lystad, M., Myrhaug, D. (1981): Skip i Sjøgang (SIS)-prosjekt.
Kjeldsen, S.P., Myrhaug, D. (1978): Kinematics and dynamics of breaking waves. STF60 A 78100.
NOAA Photo Library (1993): Mariner’s Weather Log, Fall-issue.
Statens Kartverk Sjøkartverket (1997): Den norske los, Bind 1: Alminnelige opplysninger.
Stokes , G.G. (1847): On the theory of oscillatory waves. Camb. Trans.
Torsethaugen, K. (1998): Bølger ved Stad. Sluttrapport. SINTEF rapport STF22 A982.
Trujillo, A.P., Thurman, H.V. (2005): Essentials of Oceanography, 8. utg.